Sayı Sistemlerinin Birbiri Arasında Dönüşümü

Binary (İkilik) – Decimal (Onluk) Sayı Sistemleri Dönüşümü:

Decimal’den Binary’e Dönüşüm:

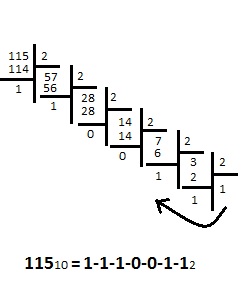
Decimal sayıyı binary sayıya dönüştürürken, bölüm 2’den küçük oluncaya kadar bölünür ve her bölme işleminden kalan alınır ve en son bölümden itibaren kalanlar sırayla soldan sağa doğru yazılır.

Örneğin 10 tabanındaki 115 sayısının, 2 tabanındaki karşılığını bulalım;

Binary’den Decimal’e Dönüşüm:

Binary sayıyı decimale dönüştürürken sağdan sola doğru 2 üzeri sıfırdan başlayarak, basamak değerine kadar üstü bir artırarak sayı basamak değeri ile çarpılır. Çıkan sonuçlar toplanır ve decimal (10 tabanlı) sayımız bulunur.

Örneğin 110101 sayımızın decimal değerini bulalım;

Hexadecimal (On Altılık) – Decimal (Onluk) Sayı Sistemleri Dönüşümü:

Decimal’den Hexadecimal’e Dönüşüm:

Decimal sayıyı Hexadecimal sayıya dönüştürürken, bölüm 16’dan küçük oluncaya kadar bölme işlemine devam edilir ve her bölme işleminden kalan alınır ve en son bölümden itibaren kalanlar sırayla soldan sağa doğru yazılır.

Örneğin 8090 decimal sayımızın, onaltı tabanına göre değerini bulalım;

Hexadecimal’den Decimal’e Dönüşüm:

Hexadecimal sayıyı Decimal’e dönüştürürken sağdan sola doğru 16 üzeri sıfırdan başlayarak, basamak değerine kadar üstü bir artırarak, sayı basamak değeri ile çarpılır. Çıkan sonuçlar toplanır ve decimal (10 tabanlı) sayımız bulunur.

Şimdi örnek olarak Hexadecimal tabanlı 36F sayısının Decimal karşılığını hesaplayalım.

Hexadecimal (On Altılık) – Binary (İkilik) Sayı Sistemleri Dönüşümü:

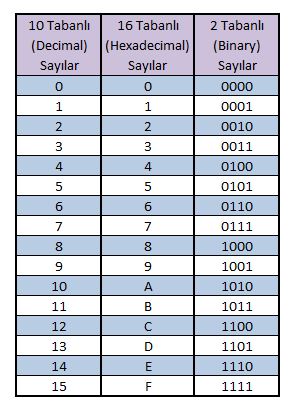
Bu iki sayı sistemi aslında önce 10 tabanlı sayı sistemine dönüştürülüp ardından hedef sayı sistemine dönüştürülür ancak bunun daha kolay bir yolu vardır. Öncelikle sayı sistemleri dersinde örnek olarak göstermiş olduğumuz tabloyu buraya ekleyelim ve ardından dönüştürme işleminin nasıl yapıldığına bakalım.

Tablomuz;

Hexadecimal’den Binary’e Dönüşüm:

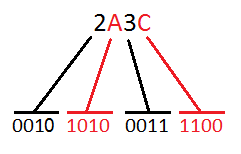
Hexadecimal’den Binary sayıya dönüşüm yaparken her basamağın yukarıdaki tablodan binary karşılığını alıyoruz ve aynı sıra ile yan yana ekliyoruz.

Örnek olarak Hexadecimal 2A3C sayısının binary karşılığını bulalım.

Binary’den Hexadecimal’e Dönüşüm:

Binary sayıdan Hexadecimal sayıya dönüşüm yaparken basamakları sağdan sola doğru dörderli gruplar halinde ayırıyoruz ve her dörderli grubun yukarıdaki tablodan Hexadecimal değerini buluyoruz.Ardından aynı sıra ile yan yana yazıyoruz.

Örnek olarak 1100111010 sayısının Hexadecimal karşılığını bulalım. Sayımızı sağdan sola doğru dörderli gruplar halinde ayırdığımızda en solda 4 basamaktan az basamak kalmışsa son grubun önündeki basamaklar sıfır kabul edilir.

Bu hesaplar yapmak zor mu geldi? Sayı Taban Dönüştürücü aracımızı deneyebilirsiniz.